Basis elektronica voor Arduino
Eén van mijn hobby's is het knutselen met de Arduino micro controller. Hieraan kan ik weinig toevoegen, want het internet staat vol met tips en trucks over dit bordje.
Wanneer ik op de diverse fora de vragen lees, merk ik dat er veel mensen zijn die weinig weten van de elektronica in en om dit bordje. Vóórdat ik het 1001e verhaal over Arduino schrijf, vertel ik eerst wat over de elektronica.
Géén moeilijke formules of zware theoretische achtergronden, die ken ik zelf ook niet.
Ik ga uit van niveau -0- ofwel: de volslagen nitwit. Dit is beslist geen minachting, ook deze mensen wil ik er bij betrekken. Elektronica en Arduino zijn leuke hobby's voor iedereen!
Dit verhaal vertel ik in delen, want uren achter elkaar lezen is niet leuk.
Deel -1- Eenheden, grootheden, wet van Ohm, serie en parallel schakelen.
Deel -2- Condensator, spoel, diode, arbeid en vermogen.
Deel -3- Transistor, digitale poorten, de Arduino (eindelijk).
Elektronica, hoe werkt dat?
Eh…. eh…. het zit in een weerstandje, maar hoe leg ik dat nou uit?
Hoe zet u de TV dan aan? Nou, je drukt op het knopje en hij floept aan!
Kijk, zo simpel is elektronica nou ook. Alles is simpel, als je het juiste knopje weet te vinden. Ook moet je wel de juiste taal kennen. Die taal is belangrijk, immers, midden in Frankrijk kom je niet ver als je geen Frans spreekt. Een taal is niets meer dan een reeks gedefinieerde klanken, die iedereen op gelijke manier interpreteert.
“Pas op! Daar staat stroom op!” “Heeft u een stopcontact voor mij?”
Twee heel normale zinnen, maar er kán geen ‘stroom’ ergens op staan, wel spanning.
Zo moet u in de winkel vragen om een wandcontactdoos, een stopcontact is héél iets anders!
Toch begrijpen we elkaar wanneer er gezegd wordt dat iets onder stroom staat.
De winkelier begrijpt meteen wat u wilt en zal vragen: inbouw, opbouw, randaarde, etc?
Waarmee ik alleen maar wil zeggen, dat er een duidelijk verschil is tussen de spreektaal en de exacte benaming.
Eérst moeten we wat afspreken over de te gebruiken termen! Dat is geen muggezifterij, maar ter voorkoming van verwarring of erger: onbegrip.
Een spanning is vergelijkbaar met de waterdruk, een spanning staat OP of OVER iets. Een stroom is vergelijkbaar met waterstroom, deze gaat DOOR iets heen. Spanning is een statisch gebeuren en stroom is dynamisch.
Een dikke buis laat makkelijker water door dan een limonaderietje. Vervolgens kan men een maat afspreken voor de moeilijkheidsgraad waarmee een water- of elektrische stroom doorgang vindt. Mijnheer Ohm heeft hier lang geleden onderzoek naar gedaan en een wetmatigheid ontdekt die naar hem is vernoemd. Ook de eenheid voor weerstand is naar hem vernoemd. Het gebruikte symbool is de Griekse letter omega: 
. Spanning wordt aangegeven met de hoofdletter -U- uitgedrukt in volt, dat weer met de hoofdletter -V- wordt aangegeven. Let op, hoofdletters, want de kleine letters worden weer voor andere zaken gebruikt. Stroom wordt met de hoofdletter -I- aangegeven. De eenheid waarin stroom wordt uitgedrukt is ampère, aangeduid met de hoofdletter -A-. De mate van 'moeilijke doorgang', de
weerstand, wordt met de hoofdletter -R- aangegeven, de eenheid is ohm .
Alle zaken op een rijtje: Grootheid Eenheid
Spanning U Volt V
Stroom I Ampère A
Weerstand R Ohm
De Wet van Ohm, is de basis van alle elektronica.
Om bij de waterkraan te blijven: hoe hoger de waterdruk, des te méér water er uit de kraan komt. Hoe wijder de kraan open staat (dus minder weerstand) des te meer water uit de kraan. Is de spanning 2 maal groter, dan zal bij gelijke kraanstand (= weerstand) ook de stroom twee maal groter zijn. (Bij de waterkraan is dit NIET zo, vergelijkingen gaan altijd een beetje mank, ook hier.) Staat de kraan twee maal verder open, dan zal bij gelijke waterdruk de stroom verdubbelen. (Ook dít is bij de waterkraan niet waar, elektronica & elektrotechniek zijn veel eenvoudiger.)
Toch een formule, die voor iedereen die de tweede klas van de lagere school, of groep 4 van het basis onderwijs met goed gevolg heeft doorlopen, moet kunnen snappen.
U = I x R ofwel spanning is stroom maal weerstand. (in eenheden: V = A x ).
Voorbeeld: de spanning 10 volt en een stroom van 2 ampère geeft een weerstand van 5 ohm.
In getalletjes: 10 = 2 x 5. Vanaf nu benoem ik de spanning, stroom, weerstand met: U; I; R.
In woorden: De stroom door een weerstand is omgekeerd evenredig met de weerstandswaarde.
De spanning is recht evenredig met de waarde van de weerstand.
Waarom zoveel aandacht hiervoor? Welnu ALLES in de elektrotechniek berust op deze wetmatigheid!
Een weerstand wordt in een schema gewoonlijk met een rechthoek aangegeven, waarbij aan de korte zijden de aansluitdraden zitten. In buitenlandse schema’s vaak als een zig-zag lijntje. Verder staan er symbooltjes in of naast. Hiermee worden nadere zaken aangegeven, zoals vermogen, gevoeligheid, regelbaarheid. Weerstanden behoren tot de passieve elementen. Dat betekent dat ze niets doen, ze ondergaan lijdzaam het elektrisch geweld dat hen wordt aangedaan.
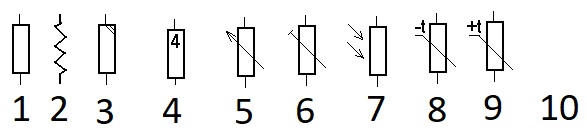
Enkele voorbeelden van weerstanden:
1 Gewone algemene tekenwijze van een weerstand
2 De Amerikaanse manier van tekenen
3 Een paar merktekens geven een nadere aanduiding, zie legenda van het schema.
4 Een cijfer komt ook voor als nadere aanduiding ook hier: zie legenda.
5 Een regelbare weerstand, potentiometer genaamd, komt voor als volumeknop.
6 Potentiometer, maar nu met schroevendraaier instelbaar, wordt instelpot genoemd.
7 Licht gevoelige weerstand, in donker hoogohmig, bij licht laagohmig. LDR
8 Temperatuur gevoelige weerstand deze wordt laagohmiger als hij warmer wordt NTC
9 Ook temperatuur gevoelige weerstand, deze wordt hoogohmiger bij warmer weer PTC
10 Ja, verzin maar een VDR voltage dependence resistor, ofwel spanningsgevoelige weerstand.
Zo zijn er eindeloos veel varianten te bedenken.
Serie schakelen
Zoals gezegd, de spanning óver de weerstand laat een stroom dóór de weerstand vloeien, hoe hoger de spanning, des te groter wordt de stroom. Het verband is de eerder genoemde wet van Ohm, U = I X R.
Een U van 10V zal door een R van 5 een I van 10 / 5 = 2A doen vloeien.
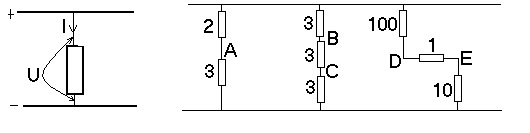
De spanning wordt hier aangegeven door de boog en de stroom door een pijl. De tweede tekening bevat een schakeling van meerdere weerstanden, het eerste deel bevat twee weerstanden, een van 2 en een van 3.
Stel, de spanning (U) is nog steeds 10V, dan loopt er een stroom van 10V / (2+3) = 2A. Op punt A is de spanning gelijk aan 2A X 3 = 6V. Maar kan ook 2A X 2 = 4V zijn. Het is maar hoe je het bekijkt, want over de weerstand van 2 staat 4V en over die andere staat 6V. Immers: 4V + 6V = 10V, de aangelegde spanning.
Meestal wordt er gemeten ten opzichte van de massa. LET OP andersom kan ook, of ten opzichte van elk ander willekeurig punt! Hier meten we ten opzichte van de – dus wordt er op punt A 6V gemeten.
Wanneer je drie gelijke weerstanden in serie schakelt, dan verdeeld de spanning zich keurig in gelijke delen over deze weerstanden. Hola! Een nieuwe kreet: “Serie schakelen” Daarmee wordt bedoeld het achter elkaar schakelen van componenten, dus ook andersoortige componenten kunnen met weerstanden in serie worden geschakeld, in deel -2- meer hierover. De stroom door de tweede tak is 10 / (3+3+3) = 3,3333A. De spanning deelt zich eveneens in drie gelijke delen, namelijk 3,333V dus op punt B wordt 6,667V gemeten en op punt C meet men 3,333V. Ook wanneer de weerstanden elk 100 zouden zijn, dan nog is de spanning op punt B=6,67V en op C meet je 3,33V. De stroom is dan veel kleiner, immers de totale weerstand van de serie schakeling is veel groter.
Reken dit zelf maar eens na. Het derde schema, Rtotaal 100+1+10 U 10V, I is:
Utot / (R100 + R1 + R10) = 10V / (100+1+10) = 90mA.
Ud = I X (R1 + R10) = 90 mA X (1 + 10) = 991 mV.
Ue = I X R10 = 90 mA X 10 = 901 mV.
Hé wéér wat nieuws, de kleine letter -m- staat vóór de eenheid. Welnu, net als bij afstanden en gewichten kan men er een maataanduiding voorzetten. Een millimeter, is een duizendste meter, een milliampère is een duizendste ampère. Zo kan men net als bij de kilometer en de kilogram, een kilo-ohm (K) hebben. Bij de groenteboer haal je een paar kilo aardappels, zo wordt er bij weerstanden ook gesproken van weerstanden van
10 kilo. Hier wordt niet het gewicht bedoeld. Ook hier is er weer verschil tussen de spreektaal en exacte taal.
Parallel schakelen
De tegenhanger van in serie schakelen is parallel schakelen. Hierbij worden de weerstanden naast elkaar geschakeld, dus elke weerstand staat op de zelfde spanning aangesloten. De totale stroom is gelijk aan de som van de afzonderlijke stromen door de elke weerstand.
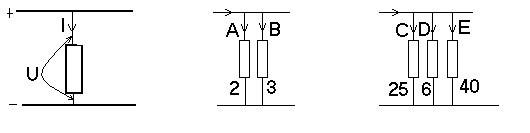
Stel, de spanning is weer 10V, door de weerstand van 2 vloeit een stroom van 5A en de naastliggende weerstand heeft een stroom van 3,33A De totale stroom die deze schakeling trekt is dan 5A + 3,33A = 8,33A. De spanning over beide weerstanden is gelijk! (U = 10V). De spanningen in punten A en B zijn beiden 10V. De stromen in A en B zijn verschillend. Ia = U / R2 = 10V / 2 = 5A. Zo is Ib = 3,33A, maar dat stond hierboven al. Daarnaast staat een schakeling met drie weerstanden, reken zelf maar de totale stroomsterkte uit die de voeding moet leveren. (Hiervoor zijn mooie formules bedacht, maar zoals beloofd, ik val u daar niet mee lastig)
Het lastigste moet nog komen, de praktijk!
In de praktijk is het niet zo mooi als hierboven, daar komen parallel en serieschakelingen door elkaar voor. Dan wordt het rekenen en nadenken, dus worden er fouten gemaakt! Dat maakt elektronica boeiend! Een goed advies: Leer van fouten van anderen, je hebt niet de tijd ze allemaal zelf te maken. Weerstanden worden door alles gevormd waardoor stroom kan vloeien, ook transistoren, spoelen, lampjes, motoren en.... mensen!!
Rekenen
De gemeten spanning, je hoeft niet te rekenen. Is dat wel goed? Of meet je die waarde omdat er wat kapot is?
Hier komt toch nog het nodige rekenwerk om de hoek kijken.
Wanneer de berekende waarde redelijk overeen komt met de gemeten waarde, dan mag je aannemen dat het wel in orde is. Zeker weet je het natuurlijk nooit, maar dat maakt elektronica zo boeiend. (Oei, ik val in herhaling.)
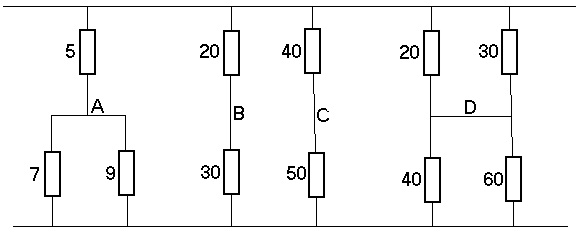
Hierboven staan drie schakelingen, een met drie weerstanden, een met twee keer twee weerstanden en daarnaast nóg een met twee maal twee weerstanden, maar dan met tussen verbinding. De cijfers zijn de weerstandswaarden in ohm. De spanning is 10V. Even terug naar de eerste parallelschakeling, het vorige schema bestond uit weerstanden van 2 en 3 De spanning was eveneens 10V en de totale stroom was 8,33A. Een enkele weerstand die eveneens 8,33A stroom zal trekken, kan berekend worden, door de spanning door de stroom te delen, immers: I = U / R Zo ook: 10V / 8,33A = 1,2. Nu is het eenvoudig om de
vervangweerstanden te berekenen, neem een fictieve spanning aan, bereken de stroom door elke weerstand, tel deze op en bereken de vervangweerstand. Dat kan eenvoudiger! ►►► Het tegenovergestelde van 'moeilijk' is 'makkelijk'. We gaan het makkelijk doen, dus als het 10 'moeilijk' is, dan is dat 1/10 = 0,1 'makkelijk'! Laat dat even rustig bezinken.
Dit omkeren komt zo vaak voor dat er op de zakjapanner een apart knopje voor is: 1/x In de elektronica wordt 'makkelijk' geleidingsvermogen genoemd. Hier ging het om weerstanden van 2 en 3 dat is 1/2 + 1/3 = 3/6 + 2/6 = 5/6 Siemens! De eenheid van geleidingsvermogen (-G-) is Siemens, weergegeven met de hoofdletter -S-. Bereken de vervangweerstand weer door het geleidingsvermogen om te keren 6/5 = 1,2. Nu hoef je niet meer zoveel delingen te maken, je telt de geleidingsvermogens bij elkaar op! Vervolgens druk je weer op het 1/x knopje om de vervangweerstand te weten, geen hoofdpijn!
Dan het schema met drie weerstanden 7 // 9 (parallel wordt vaak met // aangegeven) Rekent u zelf maar na, de uitkomst is 3,94 . Snelle controle: de uitkomst is altijd kleiner dan de kleinste weerstand. Omdat beide weerstanden ongeveer gelijk zijn, is de uitkomst ongeveer de helft van één weerstand. Dit is een snel hulpmiddel om uw berekening te controleren. Rekenmachineknopjes zijn zo klein dat je onbedoeld een verkeerd knopje kan indrukken. Nu kan je gemakkelijk deze vervangweerstand optellen bij de serieweerstand die er boven staat 5 .
Samen komt dit neer op 8,94 . De stroom is dan 10V / 8,94 = 1,12A.
Nu weet je de stroom door de bovenste weerstand, maar hoe verdeeld deze stroom zich over de onderste twee? Het enige dat we weten is de totale stroom door die twee weerstanden samen, namelijk die 1,12A. Welnu, bereken de spanning op punt A en vervolgens weer de stroom door elke weerstand.
Ua = Itot X (R7 // R9) = 1,12A X 3,94 = 4,41V. Vervolgens kan je de stroom door elke weerstand berekenen. Hier ga ik verder niet op in, dat mag je zelf doen. Ik laat een andere methode zien.
De verhouding! immers volgens de wet van Ohm verdeeld de stroom zich omgekeerd evenredig over de beide weerstanden. Dus R7 krijgt 7/(7+9)e deel, en R9 krijgt 9/(7+9)e deel. Wanneer je dat in een zakjapanner klopt, dan krijg je als antwoord: IR7 = 0,49A ; IR9 = 0.63A. Reken beide methoden nog eens na en vergelijk de antwoorden. Dit komt erg schoolmeesterig over, maar rekenen met verhoudingen en met de ohmse wet moet zonder nadenken kunnen. Niet het rekenen, maar de elektronica is de hobby!
Het tweede schemaatje:
Met de twee takken van twee weerstanden, op punt B blijkt na berekening, 6V te staan en op punt C staat 5,55V. Wanneer je de voltmeter op punten B en C zet, dan meet je 0,45V, dat is duidelijk. Nee? Aan het begin van dit verhaal vertelde ik dat de spanning ten opzichte van elk willekeurig punt gemeten kan worden. Welnu, dat doe ik nu op de punten B en C, het verschil is die halve volt. Zou ik die punten verbinden, dan is er geen spanningsverschil meer, dan loopt er wel stroom van B naar C, omdat B het hoogste niveau heeft.
Schema -3-
Stelt u zich de situatie in de derde opstelling eens voor, daar hebben we inderdaad die verbinding gemaakt, maar vloeit er stroom door die dwarsverbinding? (reken dat zelf eens uit of dat wel/niet waar is.) NEE, immers op beide punten staat met en zonder verbinding de zelfde spanning! Een heel bijzondere situatie. De verhouding tussen die weerstanden blijkt gelijk aan elkaar te zijn 20:40 = 30:60 ofwel: 20 X 60 = 40 X 30 (Kruislings vermenigvuldigen, op school geleerd!) Hiermee zijn mooie metingen te verrichten. Ik heb één onbekende (temperatuur gevoelige) weerstand, die buiten hangt. Vervolgens ga ik met drie bekende weerstanden de rest van de schakeling opbouwen.
Dan wissel ik net zo lang tot er in de dwarsverbinding géén stroom vloeit. U voelt het al, een vergelijking met één onbekende. Wanneer het om een temperatuurgevoelige weerstand gaat en ik weet welke waarde hij heeft bij elke temperatuur, dan kan ik met de weerstandsverhouding de buitentemperatuur bepalen. Een veel voorkomende schakeling.
Weerstandscode
Wanneer je weerstanden bekijkt, dan blijken het kleurrijke rakkers te zijn, geen cijfertjes waarmee je de waarde kan aflezen. Natuurlijk, effe meten, maar die kleuren zijn niet voor de sier. Elke kleur vertegenwoordigd een cijfer. De eerste twee ringen geven twee cijfers aan, de derde ring geeft het aantal nullen aan, dat achter de cijfers geplaatst moet worden. De vierde ring geeft de tolerantie aan, de afwijking van de opgegeven waarde.
Zwart 0
Bruin 1
Rood 2
Oranje 3
Geel 4
Groen 5
Blauw 6
Paars 7
Grijs 8
Wit 9
Goud 5%
Zilver 10%
Geen 20%
Een weerstand, in de kleuren rood-geel-groen-goud heeft de waarde 2,4 M 5%. Weer een kreet, M. M staat voor mega, dat wil zeggen “miljoen” de weerstand heeft een waarde van 2400000. Natuurlijk kunnen we dit zo opschrijven, maar de vergissing bij het tellen van die nullen, of er een meer of minder opschrijven is snel gemaakt. Daarom is het beter om de maataanduidingen te leren. Hieronder staan ze op een rijtje.
Terra 1 000.000.000.000
Giga 1 000.000.000
Mega 1 000.000
Kilo 1 000
Hecto 100
Deca 10
De eenheid zelf 1
Deci 0,1
Centi 0,01
Mili 0,001
Micro 0,000.001
Nano 0,000.000.001
Pico 0,000.000.000.001
Femto 0,000.000.000.000.001
In plaats van 2,4 M schrijft men ook wel eens 2M4. Bij kleine weerstanden gebruikt men wel eens E in plaats van , dus 0E4 = 0,4 De laat men vaak weg, slordig, dat wel. De gouden tolerantie ring geeft 5% aan, dwz dat de werkelijke weerstandswaarde ligt ergens tussen 2,4 +/- 120 K dus de werkelijke waarde ligt ergens tussen de 2280 K en 2520 K. Er zijn ook weerstanden met 5 ringen..... dan tellen de eerste 3 ringen en is de vierde ring de vermenigvuldigingsfactor. Dat geeft grotere nauwkeurigheid.
Volgende keer de overige passieve elementen, arbeid en vermogen.
Auteur: drejansen
/i/2003531854.png?f=fpa)
:strip_exif()/i/2003959976.jpeg?f=imagenormal)
:strip_exif()/i/2004163368.jpeg?f=imagemedium)
:quality(80)/https%3A%2F%2Fwww.want.nl%2Fwp-content%2Fuploads%2F2021%2F02%2FMotorola-G30-voor-en-achterkant.jpg)
:fill(white):strip_exif()/i/2003783772.jpeg?f=thumbmedium)
:quality(80)/https%3A%2F%2Fwww.want.nl%2Fwp-content%2Fuploads%2F2021%2F03%2FOnePlus-9.jpg)
:quality(80)/https%3A%2F%2Fwww.want.nl%2Fwp-content%2Fuploads%2F2021%2F03%2FAndroid-apps.jpg)
